The most remarkable formula in all of mathematics

I have been re-reading Genius: The Life and Science of Richard Feynman by James Gleick (hence the recent Feynman-themed post), which reminded me of a special formula in mathematics; one that Feynman himself described as follows in his famous Feynman Lectures on Physics:

In our study of oscillating systems, we shall have occasion to use one of the most remarkable, almost astounding, formulas in all of mathematics. From the physicists’ point of view, we could bring forth this formula in two minutes or so and be done with it. But science is as much for intellectual enjoyment as for practical utility, so instead of just spending a few minutes, we shall surround the jewel by its proper setting in the grand design of that branch of mathematics called elementary algebra.

This remarkable formula? Euler’s Identity:

$e^{i\pi} + 1 = 0$

In analytical mathematics, Euler’s identity (named for the pioneering Swiss-German mathematician, Leonhard Euler), is an equality renowned for its mathematical beauty, linking five fundamental mathematical constants:

The number 0, the additive identity.
The number 1, the multiplicative identity.
The number $\pi$ , which is ubiquitous in trigonometry, the geometry of Euclidean space, and analytical mathematics ( $\pi$ = 3.14159265…)
The number $e$ , the base of natural logarithms, which occurs widely in mathematical and scientific analysis ( $e$ = 2.718281828…); both $\pi$ and $e$ are transcendental numbers.
The number $i$ , the imaginary unit of the complex numbers, whose study leads to deeper insights into many areas of algebra and calculus.

The identity is a special case of Euler’s Formula from complex analysis, which states that:

$e^{ix} = \cos x + i \sin x$

for any real number $x$ . The derivation to the identity follows, as $\cos \pi = -1$ and $\sin \pi = 0$ .

Euler’s Identity reinforces the underlying beauty and interconnectedness of mathematics, pulling together three seemingly disparate areas into one simple formula, perhaps deservingly being known as “the most remarkable formula in all of mathematics”.

11 thoughts

Matthew says:

17 May 2011 at 12:21 pm

I definitely agree. If I ever win the chance to have a tattoo after inadvertently coming first in a spitting contest (or however it is that people with tattoos come by them), I shall choose this formula.

Another interesting fact that comes out of the Euler relation is the fact that i^i is a real number. I cannot decide if that happens to be mind boggling, unsurprising or useless.

Reply
Christopher says:

17 May 2011 at 8:24 pm

I’ll be a dissenter here. I prefer the related e^(2pi*i)=1.
Same idea, but cleaner.

Reply
1. Tom says:
  
  17 May 2011 at 9:28 pm
  
  True, but I suppose you can generalise to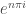 $e^{n \pi i}$ : it gives 1 for even $n$ , and -1 for odd $n$ (each increment of $\pi$ takes you halfway around the unit circle).
  
  Also, big fan of what Wolfram Alpha produces for this.
  
  Reply
Dave Donaghy says:

20 May 2011 at 11:07 am

I remember the steps from this area on to differentiating and integrating hyperbolic functions, and then realising that an extraordinary number of identities drop out as if by magic: hyperbolic correspondences to trigonometric correspondences (cos^2 + sin^2 = 1, for example) seemed like mind-boggling witchcraft the first time I saw them, and then afterwards, seemed amazingly simple.

But hindsight is very handy, and let’s not underestimate Euler’s cleverness; to quote Thomas Huxley, “How extremely stupid not to have thought of that!”

Reply
Tom says:

14 October 2011 at 1:58 pm

No blog post is complete without an xkcd comic:

Reply
Tom says:

6 November 2011 at 11:28 pm

Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don’t know what it means. But we have proved it, and therefore we know it must be the truth.

Benjamin Peirce (1809-1880) on Euler’s identity

Reply
Huw says:

31 December 2012 at 12:03 am

Also useful for calculating i^i

Reply
Tom says:

28 January 2013 at 12:19 am

Reply
thonyc says:

29 September 2013 at 8:26 pm

The whole thing was actually first discovered by Roger Cotes and not Euler ;))

Reply
1. Tom says:
  
  1 May 2014 at 8:39 pm
  
  🙂
  
  Reply
Alby says:

1 May 2014 at 8:41 pm

I wrote a blog post about understanding Euler’s equation: http://wordpress.MrReid.org/2012/07/25/understanding-eulers-identity/.

Reply